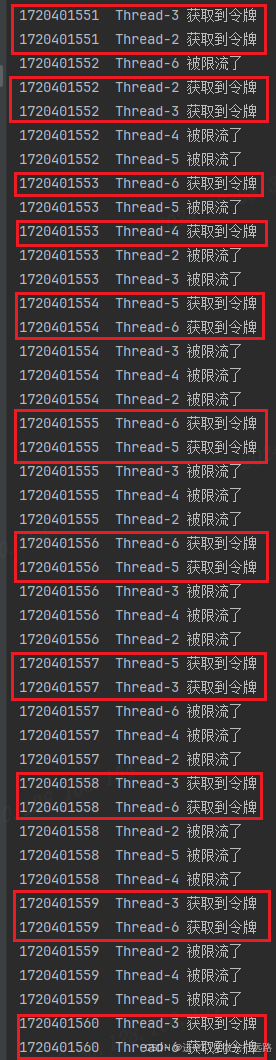
链式法则

假设你想求下面的函数的导数
$$f(x)=\sqrt{x^2+1}$$
之前学到的微分法则没求$F^{\prime }(x)$。
我们观察到 $F$ 是一个复合函数。实际上，如果我们令 $y=f(u)=\sqrt{u}$ 并且 $u=g(x)=x^2+1$，那么我们可以写成 $y=F(x)=f(g(x))$，也就是说，$F=f\circ g$。如果我们将导数解释为变化率，这看起来是合理的。把 $\frac{du}{dx}$ 视为 $u$ 相对于 $x$ 的变化率，$\frac{dy}{du}$ 视为 $y$ 相对于 $u$ 的变化率，而 $\frac{dy}{dx}$ 视为 $y$ 相对于 $x$ 的变化率。如果 $u$ 的变化速度是 $x$ 的两倍，且 $y$ 的变化速度是 $u$ 的三倍，那么 $y$ 的变化速度应该是 $x$ 的六倍，因此我们期望：
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$

链式法则 如果 $g$ 在 $x$ 处可导，且 $f$ 在 $g(x)$ 处可导，那么由 $F=f\circ g$ 定义的复合函数 $F(x)=f(g(x))$ 在 $x$ 处可导，且 $F’$ 由以下乘积给出：

$$F\prime (x)=f\prime (g(x))\cdot g\prime (x)$$

用莱布尼茨记号表示，如果 $y=f(u)$ 和 $u=g(x)$ 都是可导函数，那么：

$$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}$$

证明 设 $\Delta u$ 是对应于 $\Delta x$ 在 $x$ 上的变化，即
$$\Delta u=g(x+\Delta x)-g(x)$$
那么相应的 $y$ 的变化是
$$\Delta y=f(u+\Delta u)-f(u)$$
我们可以写成
$$\begin{array}{rl}\frac{dy}{dx}& =\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}\\ & =\underset{\Delta x\to 0}{\lim }\left(\frac{\Delta y}{\Delta u}\cdot \frac{\Delta u}{\Delta x}\right)\\ & =\underset{\Delta u\to 0}{\lim }\frac{\Delta y}{\Delta u}\cdot \underset{\Delta x\to 0}{\lim }\frac{\Delta u}{\Delta x}\\ & =\frac{dy}{du}\cdot \frac{du}{dx}\end{array}$$
(注意，因为 $g$ 是连续的，所以当 $\Delta x\to 0$ 时 $\Delta u\to 0$)

在这个推理中唯一的缺陷是，在上式中，可能会出现 $\Delta u=0$（即使 $\Delta x\ne 0$），当然，我们不能除以 $0$。不过，这个推理至少表明链式法则是成立的。

例一 求导$f(x)=\sqrt{x^2+1}$。

例二 求导$y=\sin x^2$和$y={\sin }^{2}x$。

幂法则结合链式法则 如果 $n$ 是任意实数且 $u=g(x)$ 可导，那么

$$\frac{d}{dx}(u^n)=n{u}^{n-1}\frac{du}{dx}$$

或者

$$\frac{d}{dx}[g(x){]}^n=n[g(x){]}^{n-1}\cdot g\prime (x)$$

例三 求导$y=(x^3-1{)}^{100}$。

例四 求导$f(x)=\frac{1}{\sqrt[3]{x^2+x+1}}$。

例五 求导$g(t)=(\frac{t-2}{2t+1}{)}^9$。

例六 求导$y=(2x+1{)}^5(x^3-x+1{)}^4$ 。

例七 如果 $f(x)=\sin (\cos (\tan x))$，那么

$$\begin{array}{rl}{f}^{\prime }(x)& =\cos (\cos (\tan x))\cdot \frac{d}{dx}\cos (\tan x)\\ & =\cos (\cos (\tan x))\cdot -\sin (\tan x)\cdot \frac{d}{dx}\tan x\\ & =-\cos (\cos (\tan x))\cdot \sin (\tan x)\cdot {\sec }^{2}x\end{array}$$

例八 求导$y=\sqrt{{\sec }^{3}x}$

练习

1.找到函数 $f(x)=2\sin x+{\sin }^{2}x$ 图形上切线水平的所有点。

2.如果 $F(x)=f(g(x))$ ，其中 $f(-2)=8$ ，$f\prime (-2)=4$ ，$f\prime (5)=3$ ， $g(5)=-2$ ，并且 $g\prime (5)=6$ ，求 $F\prime (5)$。

3.空气正被注入一个球形的气象气球。在任意时刻 $t$，气球的体积为 $V(t)$，其半径为 $r(t)$。

(a) 导数 $\frac{dV}{dr}$ 和 $\frac{dV}{dt}$ 分别代表什么？

(b) 用 $\frac{dr}{dt}$ 表示 $\frac{dV}{dt}$。

4.假设 $y=f(x)$ 是一条曲线，它始终位于 $x$ 轴之上，并且从未有过水平切线，其中 $f$ 在各处都是可导的。求 $y$ 的值，使得 $y^5$ 相对于 $x$ 的变化率是 $y$ 相对于 $x$ 的变化率的八十倍。

(a) 如果 $f(x)=|\sin x|$，求 $f’(x)$ 并绘制 $f$ 和 $f’$ 的图像。$f$ 在哪里不可导？

(b) 如果 $g(x)=\sin |x|$，求 $g’(x)$ 并绘制 $g$ 和 $g’$ 的图像。$g$ 在哪里不可导？